This is an example of a 1206 Chip Resistor package.

Dimensions: H = 1.40, D = 3.20 ±0.20, E = 1.60 ±0.20, L = 0.50 ±0.25

The IPC-7352 mathematical model includes the D, E and L dimensions and tolerances and the solder joint goal settings for Toe = 0.35, Heel = 0.00, Side = 0.00

Resulting pad size rounded to 2 places is   L 1.15 x W 1.80 x G 1.80

The resulting pad stack pattern must have the terminal leads on the pad stack in these conditions:

1. The Nominal Material condition of the component package & Nominal Terminal.

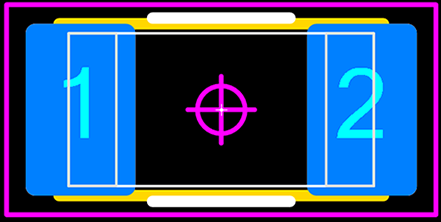
2. The Minimum Material condition of the component package & Nominal Terminal.

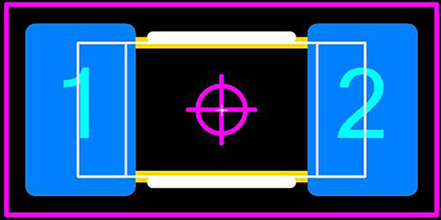
3. The Maximum Material condition of the component package & Nominal Terminal.

4. The Minimum Material condition of the component package & Minimum Terminal.

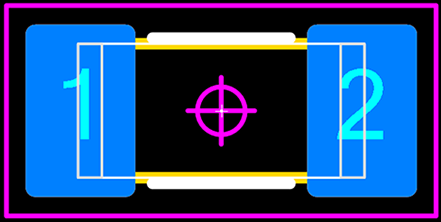
5. The Maximum Material condition of the component package & Maximum Terminal.

The resulting pad stack must have terminal leads on the pad stack regardless of every possible Material Condition possible to pass assembly inspection and meet the requirements set forth in the IPC J-STD-001 Standard and the IPC-7352 Guideline in Figure 3-3 Profile Dimensioning.

i.e.: regardless of the Component Package and Terminal Lead Material Condition, the Terminal Lead must never be exposed outside the calculated pad stack.

This is proof that the V24 Footprint Expert mathematical model illustrated in the IPC-7352 guideline achieves that goal.

Note: most component packages are created in the Nominal Material Conditions. The package tolerances play a key role in the resulting pad stack.

This footprint image represents Nominal Package Dimensions with no Package Tolerances:

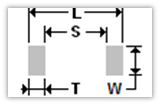
Definitions:

(All dimensions are in millimeters)

tol = tolerance;
min = minimum, max = maximum;
L = lead span, S = lead space;
T = terminal length, W = terminal width;

Example for a 1206 Chip

Lmax = 3.40, Lmin = 3.00, Ltol = length tolerance = Lmax - Lmin = 0.40
Tmax = 0.75, Tmin = 0.25, Ttol = terminal tolerance = Tmax - Tmin = 0.50
Wmax = 1.80, Wmin = 1.40, Wtol = width tolerance = Wmax - Wmin = 0.40

Smax = Lmax - (2 * Tmin) = 3.40 - (2 * 0.25) = 2.90
Smin = Lmin - (2 * Tmax) = 3.00 - (2 * 0.75) = 1.50
Stol (worst case) = Smax - Smin = 2.9 - 1.5 = 1.40

The worst-case difference between 'Smin' and 'Smax', 1.40, is statistically improbable since a simultaneous combination of extreme material conditions is considered beyond the actual range within which components are manufactured. To arrive at a more realistic tolerance range, the RMS (Root Mean Square) value is calculated using the tolerances on the dimensions involved. In this case 'L' and 'T'.

Stol (RMS) = RMS tolerance accumulation =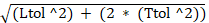
Stol (RMS) = 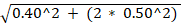= 0.81

Sdiff = difference between Stol (worst case) and Stol (RMS)
Sdiff = Stol - Stol (RMS) = 1.40 - 0.81 = 0.59

To derive a new maximum and minimum dimension for 'S' in order to determine land patterns, half of 'Sdiff' is subtracted from 'Smax' and half the 'Sdiff' is added to the 'Smin'. This technique is used so that more realistic 'S' limits are used in the land pattern equations for calculating the minimum land pattern gap between heel fillets.

Smax (RMS) = Smax - (Sdiff / 2) = 2.90 - (0.59 / 2) = 2.605
Smin (RMS) = Smin + (Sdiff / 2) = 1.50 + (0.59 / 2) = 1.795

Solving for Footprint

Definitions:

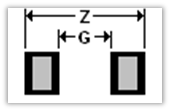
Zmax = pad span, Gmin = pad space;
Jt = toe goal (outside fillet);
Jh = heel goal (inside fillet), Js = side goal (fillet);
RMS = Root Mean Square;
F = fabrication tolerance, P = placement tolerance;

Example for the 1206 Chip

F & P were once considered as factors with typical values of F = 0.05 and P = 0.025.

They are set to zero in this example to reflect improvements in the fabrication and assembly processes and are included only to illustrate their place in the footprint calculation.

F = 0, P = 0
Jt = 0.35, Jh = 0, Js = 0

Zmax = Lmin + (2 * Jt) +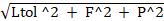
Zmax = 3.00 + (2 * 0.35) + 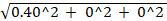= 4.10

Gmin = Smax (RMS) -(2 * Jh) -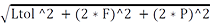
Gmin = 2.605 - (2 * 0) - 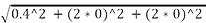= 1.79

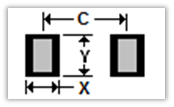
Pad Size X = (Zmax - Gmin) / 2
Pad Size X = (4.10 - 1.79) / 2 = 1.155

Pad Center-to-Center C = Zmax - Pad Size X
Pad Center-to-Center C = 4.10 - 1.155 = 2.945

Pad Size Y = Wmin + (2 * Js) + Wtol
Pad Size Y = 1.40 + (2 * 0) + 0.40 = 1.80